Drawing the Aperiodic Hat Tiling with Python and Z3

colab notebook

Numberphile recently put out a video on the discovery of the Hat Tile, which linked to an excellent blog post by David Smith about the discovery process.

In David's post, he talks about a mysterious entity "Craig’s Sat Solver" that works on assembling tilings. This piqued my curiosity: I was familiar with using an SAT solver for sudoku solutions or finding weird matricies. Could I use it to draw the hat tiling? I'm going to take a shot at showing how to tile (or fail to tile) shapes using a SAT solver (in this case, Z3)

The hat tile has an unusual property for an aperiodic tiling: it lives on a regular grid. As a result, I can enumerate all the places it is possible to put a hat or one of its component kites! This would not be so easy for, e.g., the kite and dart tiling.

First, I set up arrays that I can use to make translated or rotated copies of an object

import matplotlib.pyplot as plt
import numpy as np
import z3
from collections import defaultdict

def show_pts(pts):
  pts = pts.reshape(-1, pts.shape[-1]).transpose()
  plt.plot(pts.real, pts.imag, c=[0, 0, 0])
  plt.gca().set_aspect("equal")
  plt.show()

grid_size = 21
x, y = np.mgrid[-2:grid_size - 2, -2:grid_size - 2]
hexagon_centers = x + .5 * y + 1j * np.sqrt(3) / 2 * y
six_rotations = np.exp(1j * (np.pi /3 * np.arange(6)))

Then, I define a grid of 'kite' tiles

kite = np.array([0, .5, 1 / np.sqrt(3) * np.exp(1j * np.pi / 6), .5 * np.exp(1j * np.pi / 3), 0])
kites = kite[None, None, None, :] * six_rotations[None, None, :, None]
kites = kites + hexagon_centers[:, :, None, None]
show_pts(kites[:5, :5])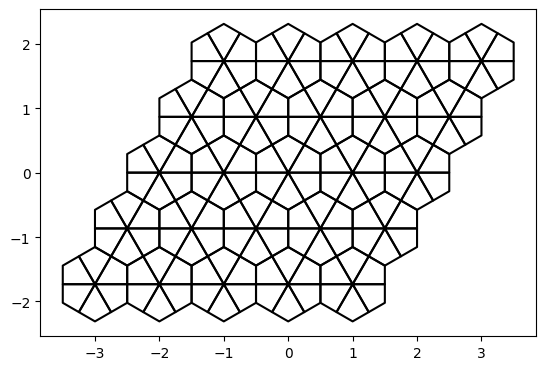

The hat is composed of 8 of these kites

indices = [
    [2, 2, 2, 2, 2, 2, 1, 1], #row
    [2, 2, 2, 2, 1, 1, 2, 2], #col
    [1, 2, 3, 4, 0, 1, 5, 4]  #rotation
    ]
hat = kites[indices[0], indices[1], indices[2], :]
show_pts(hat)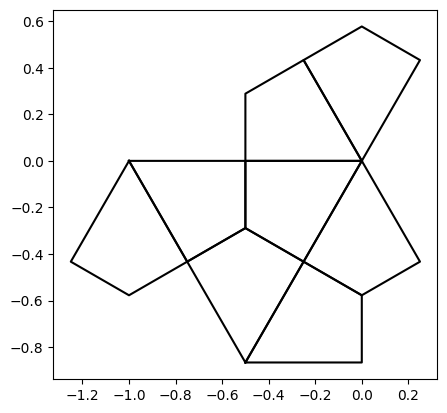

Next, I collect all possible hats into an i x j x θ x kite-in-hat x vertex-in-kite array. I then flatten this array to hat-index x kite-index x vertex-in-kite since I don't need the grid structure anymore- I just want a list of hat tiles.

hats = hat[None, :, :] * six_rotations[:, None, None]
hats = np.concatenate([hats, np.real(hats) - 1j * np.imag(hats)])
hats = hats[None, None, :, :, :] + hexagon_centers[:, :, None, None, None]
hats = np.reshape(hats, (-1, len(hat), 5))

Now it's time to set up our z3 solver. I want to pick a subset of all possible hats such that every kite is in exactly one hat. To do this, I compute every kite center, and create a map from kite centers to lists of hats that cover them. (Why do I identify kites by their center instead of by their edges?)

hat_centers = np.mean(hats, axis=-1)
hat_centers = np.round(hat_centers, 2)
hats_with_point = defaultdict(lambda: [])
for hat_index, centers in enumerate(hat_centers):
  for loc in centers:
    hats_with_point[loc] += [hat_index]

We are ready to create a tiling with Z3. I tell Z3 to keep track of a boolean value for each possible location for a hat tile.

hat_present = [z3.Bool(f"hat{i}") for i in range(len(hats))]
s = z3.Solver()

Then I input our tiling rules into the solver. In the first loop, I require that every kite must be a member of at most one hat. In the second loop, I require that kites in the interior of the region that I am tiling must be a member of at least one hat.

max_pop = max(len(c) for p, c in hats_with_point.items())
full_points = np.array([p for p, c in hats_with_point.items() if len(c) == max_pop])
all_points = np.array([p for p, c in hats_with_point.items()])
def atleastone(solver, bools):
  solver.add(z3.Or(bools))
def atmostone(solver, bools):
  #solver.add(z3.PbLe([(x,1) for x in bools], 1))
  for i, b1 in enumerate(bools):
    for j, b2 in enumerate(bools):
      if i > j:
        solver.add(z3.Not(z3.And(b1, b2)))
for p in all_points:
  atmostone(s, [hat_present[i] for i in hats_with_point[p]])
for p in full_points:
  atleastone(s, [hat_present[i] for i in hats_with_point[p]])
print(s.check())

Here, I wanted to use the built in function for counting the number of Bools that are true, PbLe, but it caused performance to tank. Manually specifying that each pair of hats covering a point cannot both be true somehow solves much faster. s.check computes a value for each boolean that together satisfy all constraints. All that's left is to plot the tiling.

This is the place to be creative, but instead I just drew the outline of each hat in black.

m = s.model()
chosen_hats = np.array([z3.is_true(m[h]) for h in hat_present])
hat = np.round(hat, 2)
segments = np.concatenate([hat[:, 1:, None], hat[:, :-1, None]], axis=2)
segments = segments.reshape(-1, 2)
reversed_segments = set(((seg[1], seg[0]) for seg in segments))
outline = np.array([l for l in segments if tuple(l) not in reversed_segments])
outlines = outline[None, :] * six_rotations[:, None, None]
outlines = np.concatenate([outlines, np.real(outlines) - 1j * np.imag(outlines)])
outlines = outlines[None, None, :, :, :] + hexagon_centers[:, :, None, None, None]
outlines = np.reshape(outlines, (-1, len(outline), 2))
result = outlines[np.array(chosen_hats), :]
result = result.reshape(-1, 2)
plt.plot(result.imag.transpose(), result.real.transpose(), c=[0, 0, 0])
plt.ylim(6, 17)
plt.xlim(-1, 15)
plt.gca().set_aspect("equal")
plt.show()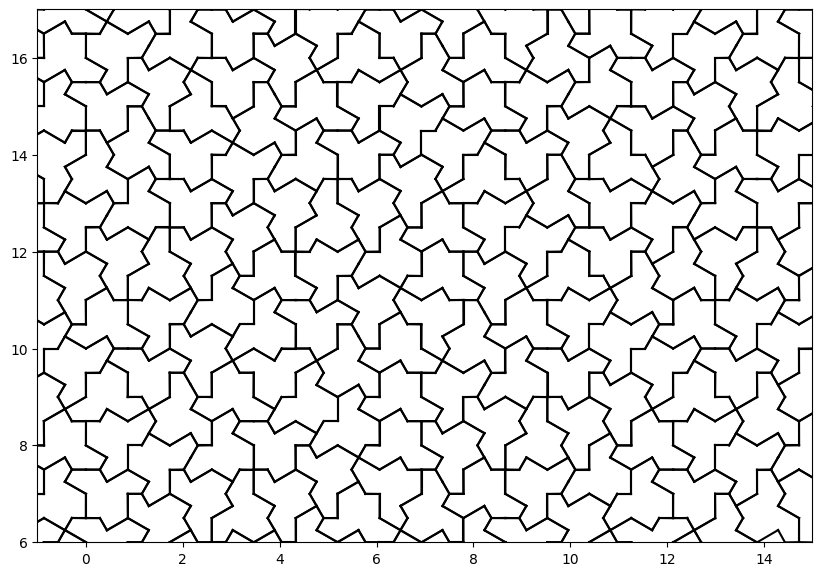

To run the code in the cloud and try variations, head to this colab notebook!

External Links:

https://www.nhatcher.com/post/on-hats-and-sats/