In our toy problem, the images we want to register, , are diffeomorphisms.
To register them, we want to find such that .
So, .
A neural network that can compute will have all the equivariances of .
Transformers naturally implement function inversion
The Key, Query, Value attention mechanism naturally lends itself to implementing function inversion in a matter appropriate for representing . As a first demo, we will invert the function
x = torch.arange(0, 1, 1/100)
x = x[None, None, :]
y = x**2First, we process our function inputs and outputs into feature vectors. These representations are chosen so that when .
scale_weight = (torch.randn(100) * 59)[:, None, None]
scale = torch.nn.Conv1d(1, 100, 1, bias=True)
with torch.no_grad():
scale.weight[:] = scale_weight
ft_x = torch.sin(scale(x))
ft_y = torch.sin(scale(y))plt.imshow(ft_x[0])
plt.imshow(ft_y[0])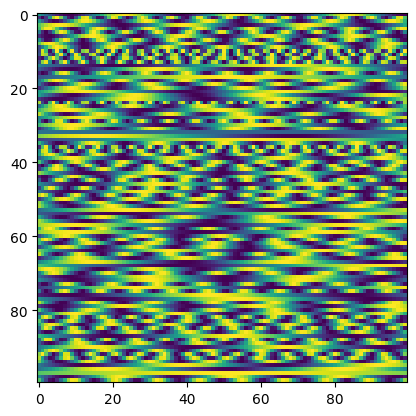

Then, do an attention, with function outputs as Keys, function inputs as Values, and the values that we want to pass to the inverted function as Queries.
attention = torch.nn.functional.softmax((ft_x.permute(0, 2, 1) @ ft_y), dim=2)
plt.imshow(attention.detach()[0])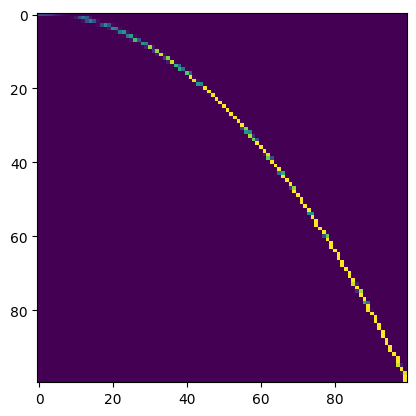
output = attention @ x.permute(0, 2, 1)
plt.plot(output[0].detach())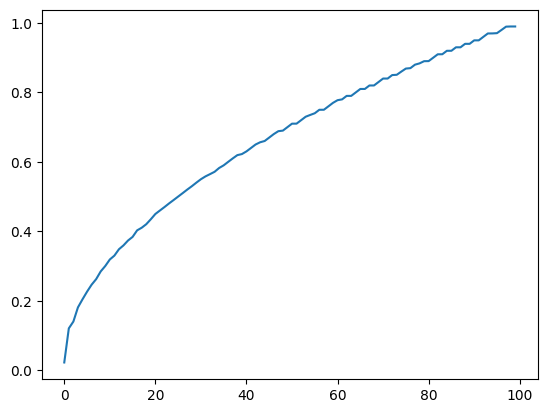
Voila, the graph of .
Registering two images using a neural network
We define some (1-D) images to register:
Image A is
Image B is
A = torch.cos(.5 * torch.pi * x)
B = x + .07 * torch.sin(3 * torch.pi * x)
plt.plot(A[0, 0])
plt.plot(B[0, 0])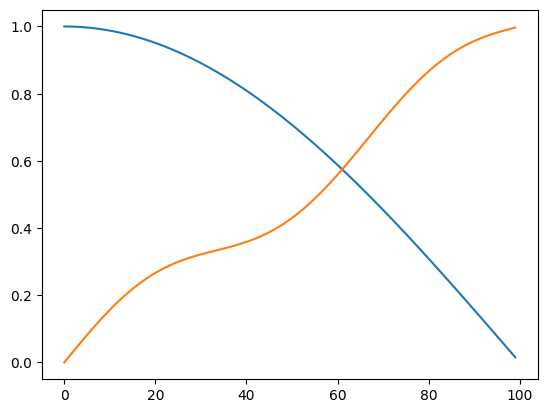
We know analytically that A and B are registered by
We create a neural network that inverts A and applies the result to B, and verify that our neural network correctly implements on this specific example.
class AttentionRegistration(torch.nn.Module):
def __init__(self):
self.x = torch.arange(0, 1, 1/100)
self.x = self.x[None, None, :]
scale_weight = (torch.randn(100) * 59)[:, None, None]
self.scale = torch.nn.Conv1d(1, 100, 1, bias=True)
with torch.no_grad():
self.scale.weight[:] = scale_weight
def featurize(values):
values = self.scale(values)
return torch.sin(values)
def forward(A, B):
ft_A = self.featurize(A)
ft_B = self.featurize(B)
attention = torch.nn.functional.softmax((ft_B.permute(0, 2, 1) @ ft_A), dim=2)
output = attention @ x.permute(0, 2, 1)
return output
ar = AttentionRegistration()
XiAB = ar(A, B)
plt.plot(XiAB[0].detach())
plt.plot((torch.arccos((x + .07 * torch.sin(3 * torch.pi * x))) * 2 / torch.pi)[0, 0])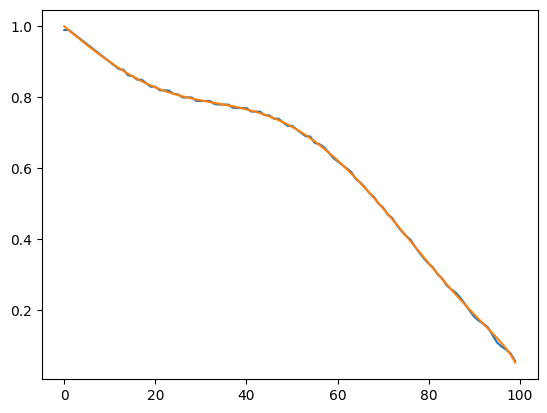
Our neural network produces the map which we proved registers A to B.