Atlas registration work
Making an atlas using a dataset and a registration network trained using MSE turns out to be relatively straightforward.
In 2D, I produced a colab notebook demonstrating that this works. 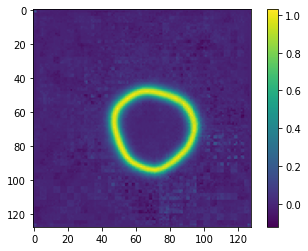
There are several questions that need answers, which the 2D work leaves ambiguous:
Whether to optimize the atlas based on the similarity, or the all-up loss
Whether to initialize the atlas randomly, or with the mean of the dataset
Whether to use a penalty on the average displacement of each pixel
Notably, this last strategy works extra well in 2-D, both producing an atlas with close to zero mean displacement as well as regularizing the intensity of the image in the LNCC case.
The LNCC case is relavant: It is needed for cross-modality registration, which marc wants for registering pairs like u
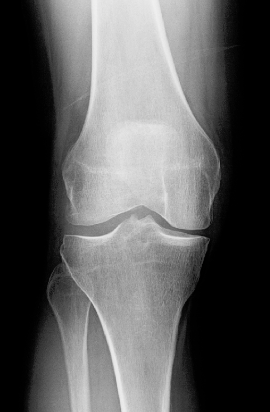

Atlas registration in 3D
Roughly, in 3-D using MSE works well, especially in the setting MSE + mean-initialize + all_loss
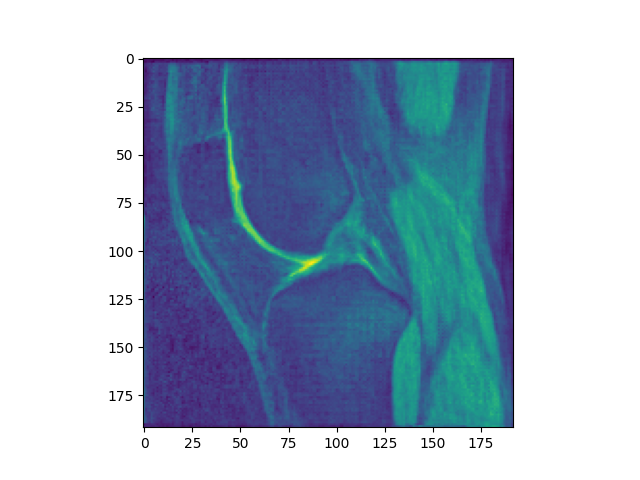
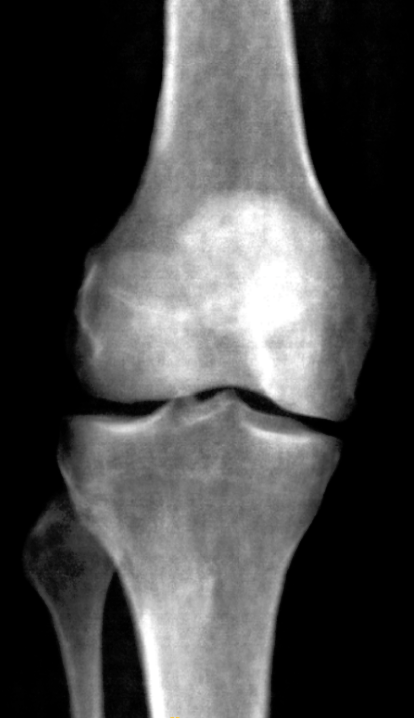
However, using LNCC, the results are distinctly cursed, even if mean inititialized. Notably, this happens without crazy intensity drift.
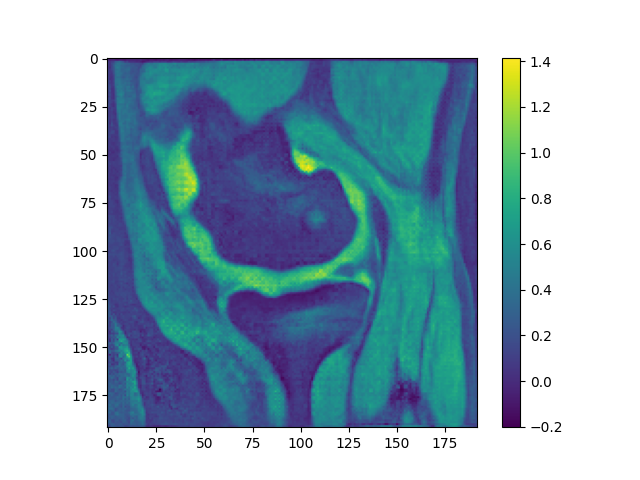
Look at this whacky patella:
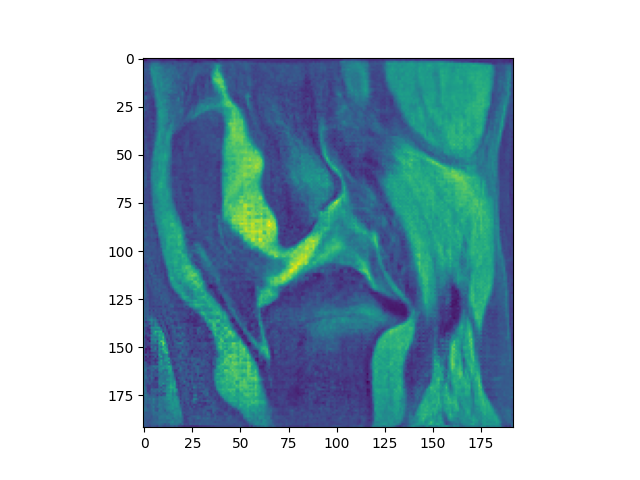
Atlas performance in 3D
Using the atlas generated by the mean squares technique, we can compare the performance of the ICON_atlas algorithm using the old, pregenerated atlas to the performance of that same algorithm using the new, icon generated atlas in terms of DICE.
We get the results:
No atlas: (register directly)
71.3
Old atlas: (currently in use in oai_analysis_2)
DICE 70.6
New atlas:
DICE 71.6
Regularizing LNCC in 2D
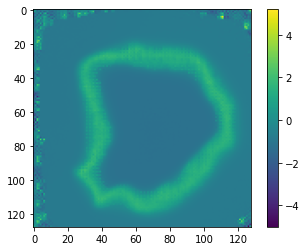
In 2-D, the atlas generated by (rand_init, LNCC, all_loss) looks like this:
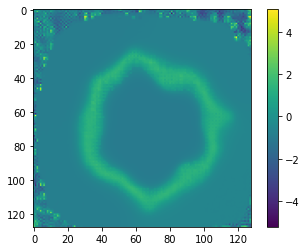
The atlas generated by (rand_init, LNCC, all_loss + 40 * squared mean pixel disp) looks like this:
 _ The atlas generated by (mean_init, LNCC, all_loss + 900 * squared mean pixel disp) looks like this:
_ The atlas generated by (mean_init, LNCC, all_loss + 900 * squared mean pixel disp) looks like this:
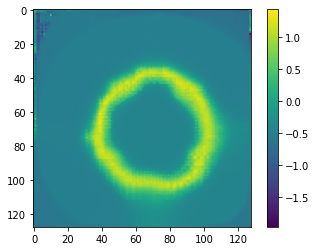
The atlas generated by (mean_init, LNCC, all_loss):
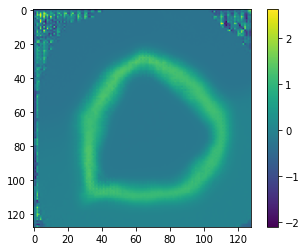
I'm not sure what to make of this: making an atlas out of LNCC seems hard, and the cursed wobbles seem to be a general principle.
side question: is penalizing the mean jacobian more powerful?
finally, we can actually regularize LNCC by (mean_init, LNCC, all_loss + 900 * sq pix disp, extra long training) as demonstrated in this notebook.
notebook for live investigating
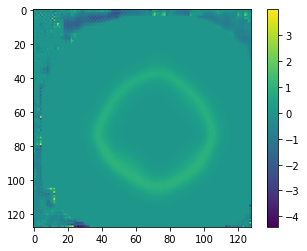
Bringing Mean displacement penalty to 3D:
Marc's math:
Then the variation with respect to u_i is:
And therefore the gradient is:
discuss
Lung Experiments
DICE of fine tuning highest resolution network for 50 steps on each OAI test pair:
74.91
Back to Reports